Cálculo curvatura en una esfera
Esquema
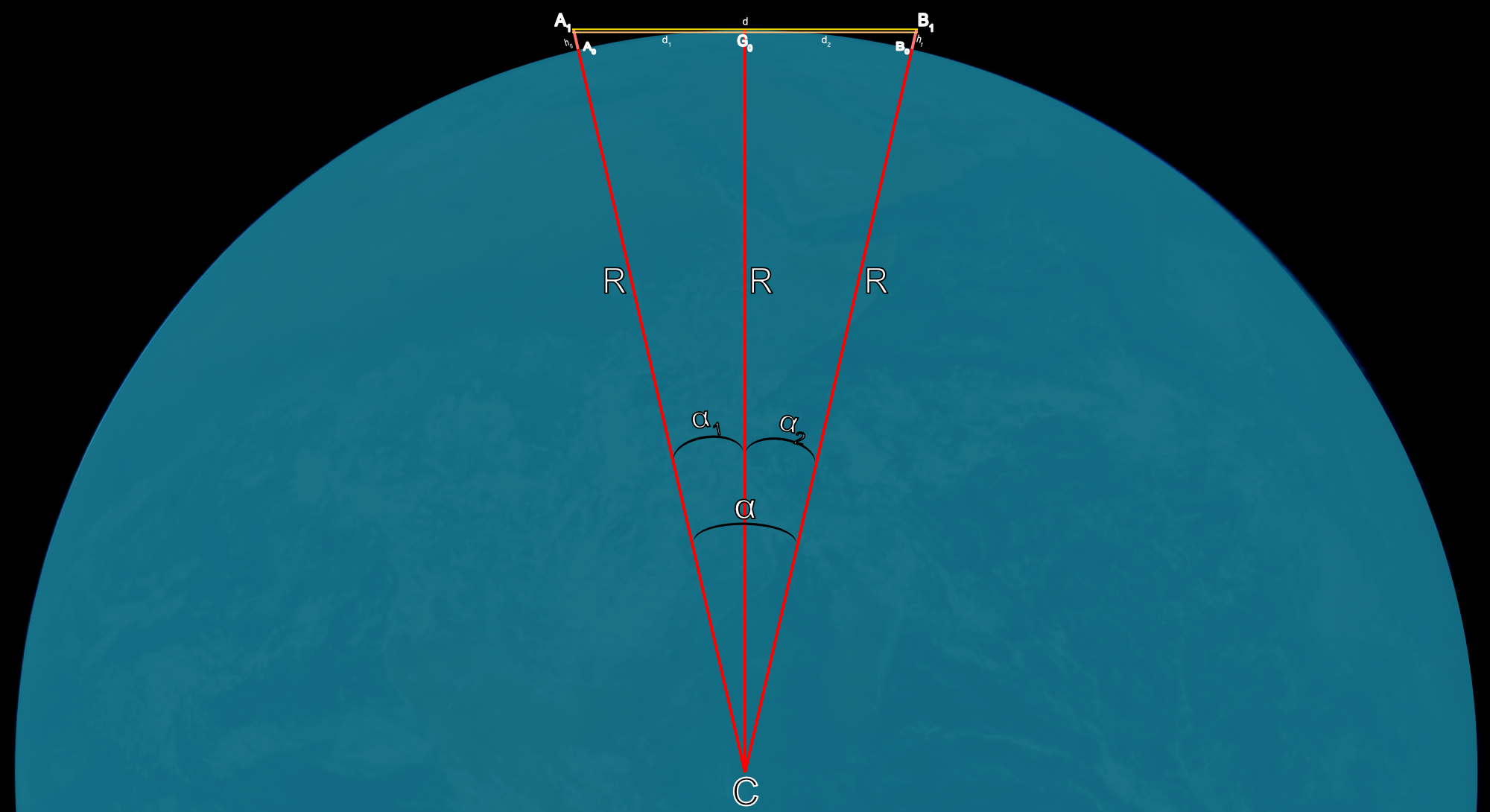
- Ángulos:
- α: variación angular $\overline{\rm A_0 B_0}$.
- α1: variación angular $\overline{\rm A_0 G_0}$.
- α2: variación angular $\overline{\rm G_0 B_0}$.
- Distancias:
- d: distancia desde $\overline{\rm A_1 B_1}$.
- d1: distancia desde $\overline{\rm A_1 G_0}$.
- d2: distancia desde $\overline{\rm G_0 B_1}$.
- h0$: altura del observador, $\overline{\rm A_0 A_1}$.
- h1: altura oculta por curvatura, $\overline{\rm B_0 B_1}$.
- R: radio del círculo / esfera.
- Puntos:
- A0: base del observador.
- A1: parte alta del observador.
- B0: base del objeto.
- B1: parte alta del objeto.
- G0: corte por curvatura, límite geométrico.
- C: centro del círculo / esfera.
Representación de una esfera de radio (R=6371 Km) con las distancias y alturas asociadas.
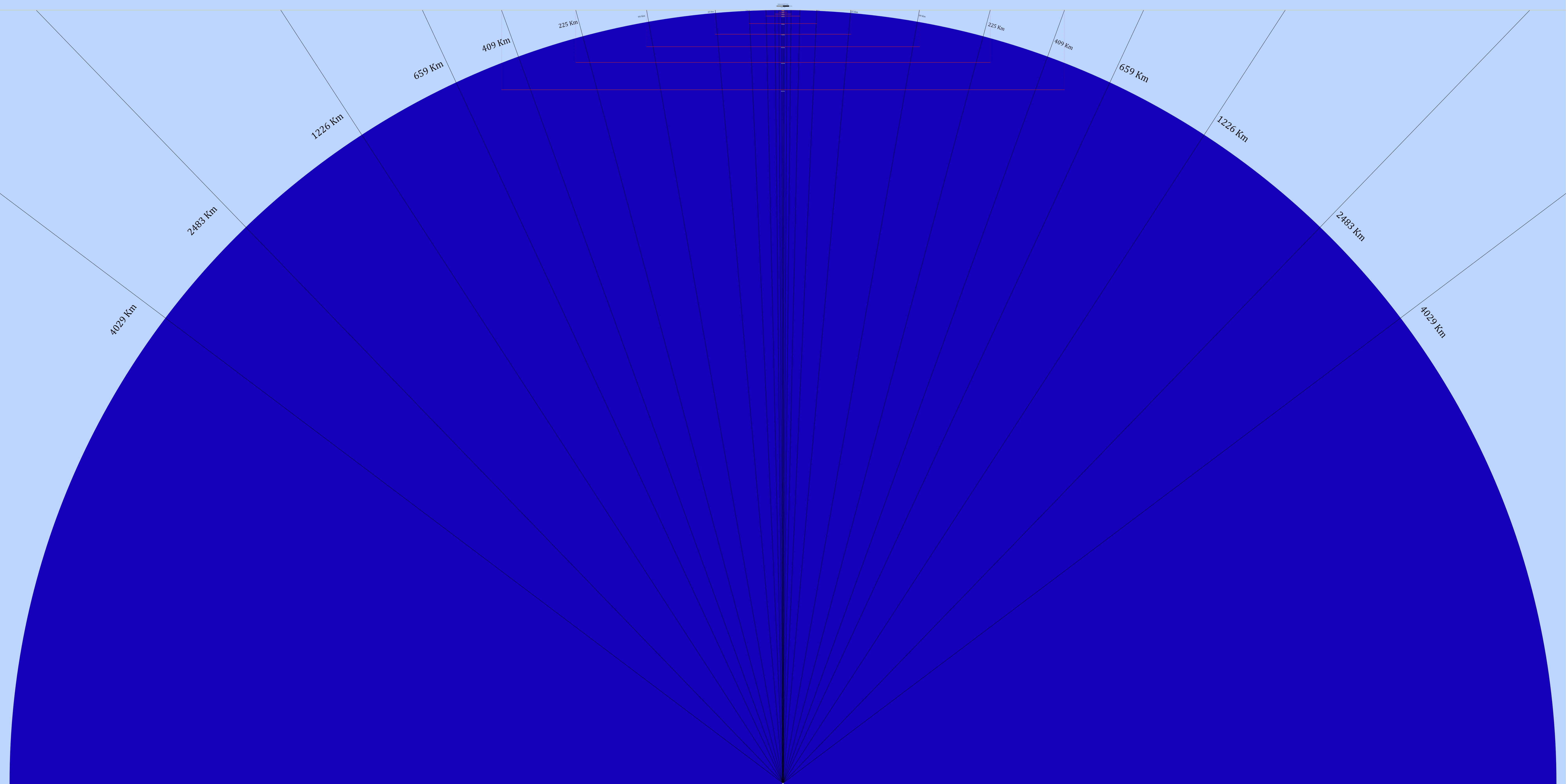
Método de cálculo
1. Teorema de Pitágoras con altura inicial
-
Teorema de Pitágoras: $$a²+b²=c² \Rightarrow c=\sqrt{a²+b²}$$
-
Siendo (a=d1, b=R, c=R+h0): $$d_1^2+R^2=(R+h_0)^2 \Rightarrow d_1=\sqrt{(R+h_0)²-R²}=\sqrt{h_0^2+2Rh_0}$$
-
Y también a=d2, b=R, c=R+h1, para d=d1+d2 -> d2=d-d1 $$d_2^2+R^2=(R+h_1)^2 \Rightarrow h_1=\sqrt{d_2^2-2Rh_1}=\sqrt{(d-d_1)^2-2Rh_1}$$
-
Función matemáticade la curvatura para una esfera de R=6371 Km sobre la superficie. La distancia (eje Y) depende de la altura oculta (eje X): $$d=\sqrt{h^2+12742 \cdot h}$$
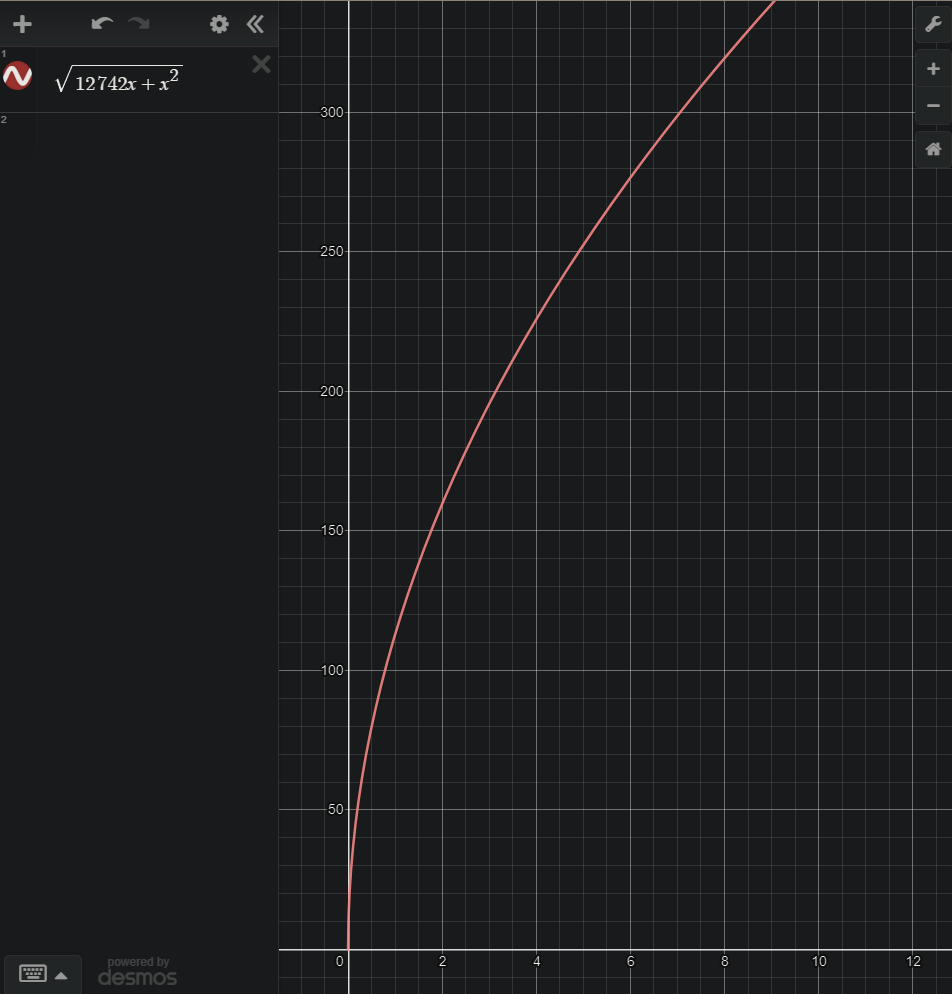
Ejemplo: para h=1 Km: $$d=\sqrt{1^2+12742}=112.885 Km$$


2. Perímetro de un círculo
- Perímetro de un círculo $$C=2 \pi R$$
- Ángulo por unidad (radianes por kilómetro): $$\alpha_{Km}=\frac{\alpha_T}{C}=\frac{2 \pi}{2 \pi R} = \frac{1}{R}$$
- Ángulo para distancia (d) dada: $$\alpha=\alpha_{Km} \cdot d$$
- Cálculo de la altura h:
$$h = r \cdot (1 - cos(\alpha)) = r \cdot \left(1-cos\left(\frac{d}{R}\right)\right)$$
- Ejemplo: para d=113 Km $$ h = 6371 \cdot \left(1 - cos \left(\frac{113}{6371} \right)\right) = 1.002 Km$$
3. Trigonometría
- Fórmulas $$sen^2(α)+cos^2(α)=1$$ $$cos(α)=\frac{R}{R+h} \approx \frac{R-h}{R}$$ $$sen(α)=\frac{d}{R+h}$$ $$tg(α)=\frac{d}{R}$$
- Despejando la tangente y el coseno $$tg(α)=\frac{d}{R} \Rightarrow \alpha=arctg(\frac{d}{R})$$ $$cos(α)=\frac{R}{R+h} \Rightarrow h=R \cdot (sec(α)-1)$$ Sustituyendo para d=113 Km, hallar α y h: $$\alpha=arctg(\frac{113}{6371})$$ $$h=6371 \cdot\left(\frac{1}{arctg(\frac{113}{6371})}-1\right)=1.187 Km$$
- Usando la segunda fórmula del coseno $$cos(\alpha)=\frac{R-h}{R} \Rightarrow h=R \cdot (1-cos(\alpha))$$ Sustituyendo para d=113 Km: $$h=6371 \cdot \left(1 - cos\left(arctg \left(\frac{113}{6371}\right)\right)\right)=1.001 Km$$
Programas en Python
1. Teorema de Pitágoras
# Pythagorean theorem with observer height, input (d, h0, R) & output (h1)
from numpy import*
# Data: R, h0, h1, d, d1 with same unit (e.g. Km)
## hR: elevated area along all the distance. Example: if the observer and object are separated at the shore of a lake at 200 m of altitude,
## the height is the same along all the distance and is not at sea level, so would be hR = 0.2 Km. (Default hR = 0, sea level)
# User data in same unit (Km)
d = 30
h0 = 0.01 # h0 = 0.01 Km = 10 m
hR = 0
R = 6371 + hR
# Pythagorean theorem:
# d2 = d - d1, (R+h0)^2=d1^2+R^2 and (R+h1)^2=d2^2+R^2
d1 = sqrt(h0**2+(2*R*h0))
h1 = sqrt((d-d1)**2+R**2)-R
print("The distance to the geometrical horizon is %.3f Km and the hidden height is %.3f Km" % (d1, h1))
2. Trigonometría
# Trigonometry at sea level
from numpy import*
# Data: R, h1 (same units, e.g. Km)
R = 6371
h1 = array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]) # Target hidden height
# Target distance : d
d = R*arccos(R/(R+h1))
# Print the result
for i in range(len(h1)):
print("The hidden height is %.1f Km for a distance of %.2f Km" % ((h1[i], d[i])))
3. Perímetro de un círculo
# Angle of curvature of a given perimeter, at sea level.
from numpy import*
## Input data (same units, e.g. Km)
R = 6371
C = 2*pi*R # C=12742*pi=40030.14 Km
d = 30
# Angle (in degrees) per unit, convert python defaults radians to degrees
alfa_km = 2*pi/C
# Angle for given distance (d):
alfa = alfa_km*d
# Calculus of the hidden height h1:
h1 = R*(1-cos(alfa))
print("At a distance of %.2f km at sea level the hidden height by curvature is %.2f km." % (d, h1))
Conclusión
Los métodos mencionados para realizar el cálculo varían pero todos dan un resultado muy parecido. Para alturas muy elevedas los cálculos por Pitágoras no son tan correctos y aparace el segundo resultado (negativo) de la raíz cuadrada. Además hay que tener en cuenta que en el modelo esférico no se podría ver nada más allá de la distancia del radio, ya que la cara visible de la esfera es como máximo un ángulo de 90º desde la vertical.