
Para contestar a la pregunta «¿Qué es un sistema de numeración?» también llamado sistema numérico o base X (donde X es un número) empezaremos por su definición. Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos.
Matemáticamente se expresa como: $$N = (S, R)$$ donde, N: es el sistema de numeración considerado. S: es el conjunto de símbolos permitidos en el sistema. R: son las reglas que nos indican qué números y qué operaciones son válidos en el sistema.
Se clasifican en dos grandes grupos: posicionales y no-posicionales:
- En los sistemas posicionales el valor de un dígito depende tanto del símbolo utilizado, como de la posición que ese símbolo ocupa en el número. Es el caso de los números romanos (I, II, III, IV, V, VI, VII…).
- En los sistemas no-posicionales los dígitos tienen el valor del símbolo utilizado, que no depende de la posición (columna) que ocupan en el número. Por ejemplo los números arábigos modernos.
Nota: tanto los números arábigos como los romanos son números del sistema decimal (base diez).
Los sistemas de numeración son la base para poder contar las cosas, lo material o en general lo cuantitativo. Sin embargo para contar no hace falta hacer uso de los números, los animales pueden contar, un perro pastor sabe si faltan ovejas en su rebaño o no y lo hace empleando la visión. La forma básica de contar es haciendo uso de los sentidos (la vista, el tacto, el oído, el gusto o el olfato) interactuando con objetos, formas, colores u olores. Mientras a un nivel más complejo sería hacer uso del cálculo matemático, empleando para ello los sistemas de numeración con sus reglas y sus números correspondientes.
¿Y qué significa o representa un número? Pues hay dos formas de definirlo:
- De forma abstracta, es el elemento fundamental de sistema numérico (conjunto provisto de dos operaciones que verifican ciertas condiciones relacionadas con las propiedades conmutativa, asociativa y distributiva).
- De forma concreta, representa una cantidad métrica o un número ordinal que ocupa una posición dentro de un orden de una serie determinada.
El número gráficamente se escribe mediante símbolos definidos por el sistema de numeración, estos símbolos o grafemas se denominan cifras, y si están formados por un solo carácter se llama dígito. Por ejemplo 2048 es una cifra del sistema de numeración arábigo, y sus cifras son el dos (2), el cero (0), el cuatro (4), y el ocho (8). Los números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 son dígitos ya que están formados por una sola cifra.
A lo largo de la historia la mayor parte de las civilizaciones han hecho uso del sistema en base diez, sin embargo algunas civilizaciones como los Mayas o los Aztecas hacían uso de un sistema vigesimal (base veinte).
“En la actualidad el sistema arábigo es el más usado para representar los números. Se les llama «arábigos» porque los hispano-árabes de al-Ándalus los introdujeron en Europa a través de su acción cultural, aunque su invención surgió en la India. El mundo le debe a la cultura india el invento trascendental del sistema de numeración posicional, así como el descubrimiento del 0 (cero), llamado śūnya (shuunia) o bindu en lengua sánscrita, sin embargo los mayas también conocieron tanto el 0 como la numeración posicional.” [[#Bibliografía de Wikipedia | Cita 4]]
En cambio hay muchos más sistemas en uso de lo que podríamos esperar, está el binario (en computación), ternario (comparación lógica y ordenadores ternarios), cuaternario (en computación cuántica), octal (informática), hexadecimal (en ordenadores). Los minutos y segundos que se repiten cada 60 o las horas cada 12, no forma un sistema de numeración propio ya que hacen uso del sistema decimal. Se trata de la aplicación de la aritmética modular, en este caso de módulo 60 y módulo 12.
El Teorema fundamental de la numeración establece la fórmula general para construir un número N, con un número finito de decimales en un sistema de numeración posicional de base b, tal que:
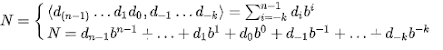
donde, N : número válido en el sistema de numeración. b : base del sistema de numeración, número de símbolos permitidos en el sistema. d: dígito, símbolo cualquiera de los permitidos en el sistema de numeración. n: número de dígitos de la parte entera, incluído el cero (0). k: número de dígitos de la parte decimal.
| Posición | … | 2 | 1 | 0 | -1 | -2 | … |
|---|---|---|---|---|---|---|---|
| Valor base | … | b² | b¹ | b⁰ | $$b^{−1}$$ | $$b^{−2}$$ | … |
| Dígito | … | d² | d¹ | d⁰ | $$d^{−1}$$ | $$d^{−2}$$ | … |
| Ej: base diez | … | 100 | 10 | 1 | 0.1 | 0.01 | … |
Como conclusión, las matemáticas no se inventan se descubren como método para expresar de forma abstracta los cambios en la naturaleza, lo que sí se inventa es el método de expresarlo pero no el contenido.