Sphere curvature calculator
Scheme
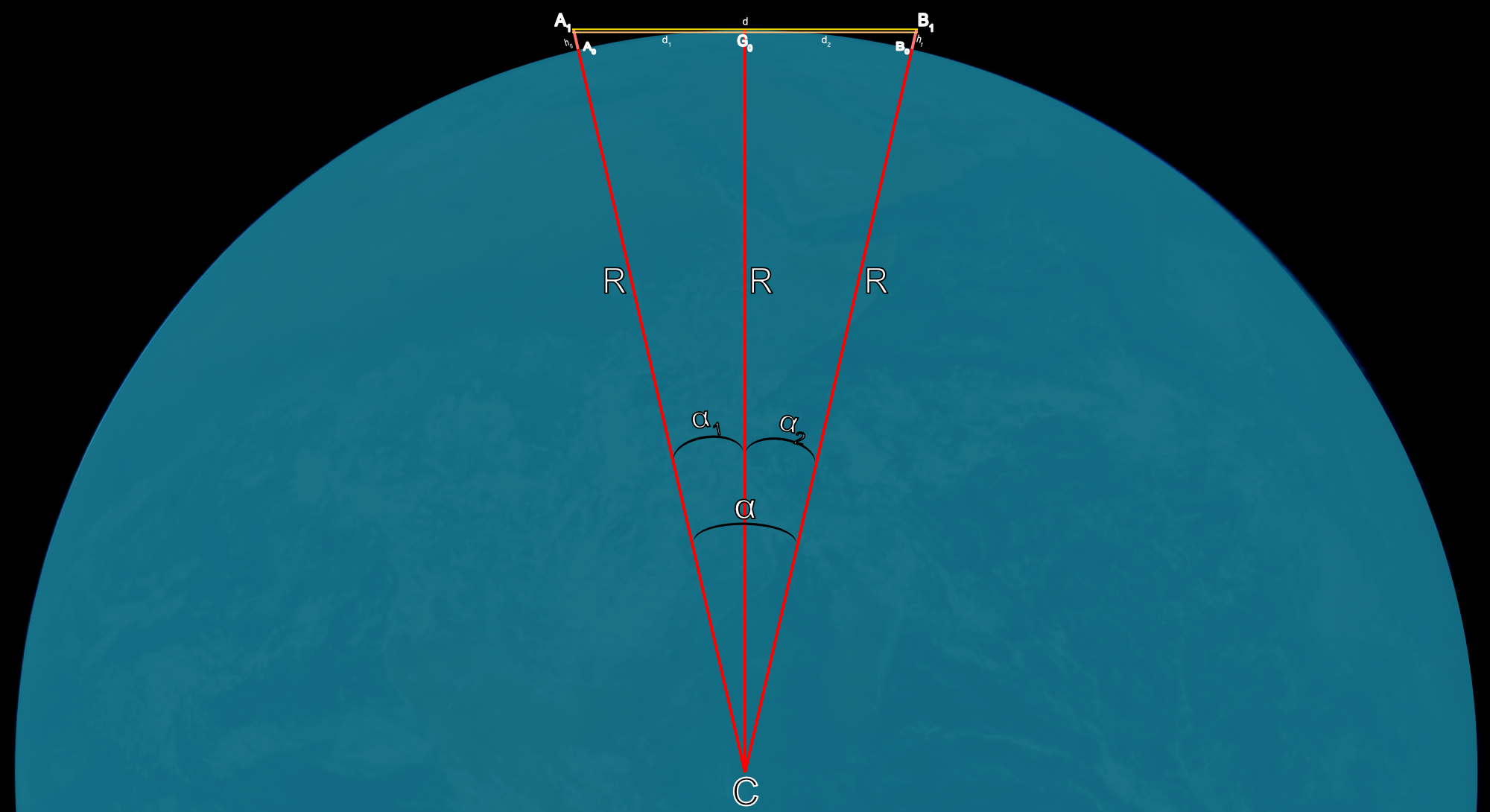
- Ángulos:
- α: angle variation $\overline{\rm A_0 B_0}$.
- α1: angle variation$\overline{\rm A_0 G_0}$.
- α2: angle variation $\overline{\rm G_0 B_0}$.
- Distancias:
- d: distance from $\overline{\rm A_1 B_1}$.
- d1: distance from $\overline{\rm A_1 G_0}$.
- d2: distance from $\overline{\rm G_0 B_1}$.
- h0$: observer height, $\overline{\rm A_0 A_1}$.
- h1: target hidden height, $\overline{\rm B_0 B_1}$.
- R: radius of the sphere / circle.
- Puntos:
- A0: base of the observer
- A1: top of the observer
- B0: base of hidden object
- B1: top of hidden object
- G0: curvature shear, geometric limit
- C: center of the circle / sphere
Representation of a sphere of radius (R=6371 Km) with distances and heights.
Calculation methods
There are three main methods to solve the geometrical problem. Here you can see the code to solve the math problem with python. You can compile online (online-python.com) or local with python installed.
1. Pythagorean Theorem with observer height
-
Pythagorean Theorem: $$a²+b²=c² \Rightarrow c=\sqrt{a²+b²}$$
-
Where (a=d1, b=R, c=R+h0): $$d_1^2+R^2=(R+h_0)^2 \Rightarrow d_1=\sqrt{(R+h_0)²-R²}=\sqrt{h_0^2+2Rh_0}$$
-
And also a=d2, b=R, c=R+h1, para d=d1+d2 -> d2=d-d1 $$d_2^2+R^2=(R+h_1)^2 \Rightarrow h_1=\sqrt{d_2^2-2Rh_1}=\sqrt{(d-d_1)^2-2Rh_1}$$
-
Mathematical function of the curvature for a sphere of R=6371 km above the surface. The distance (Y-axis) depends on the hidden height (X-axis): $$d=\sqrt{h^2+12742 \cdot h}$$
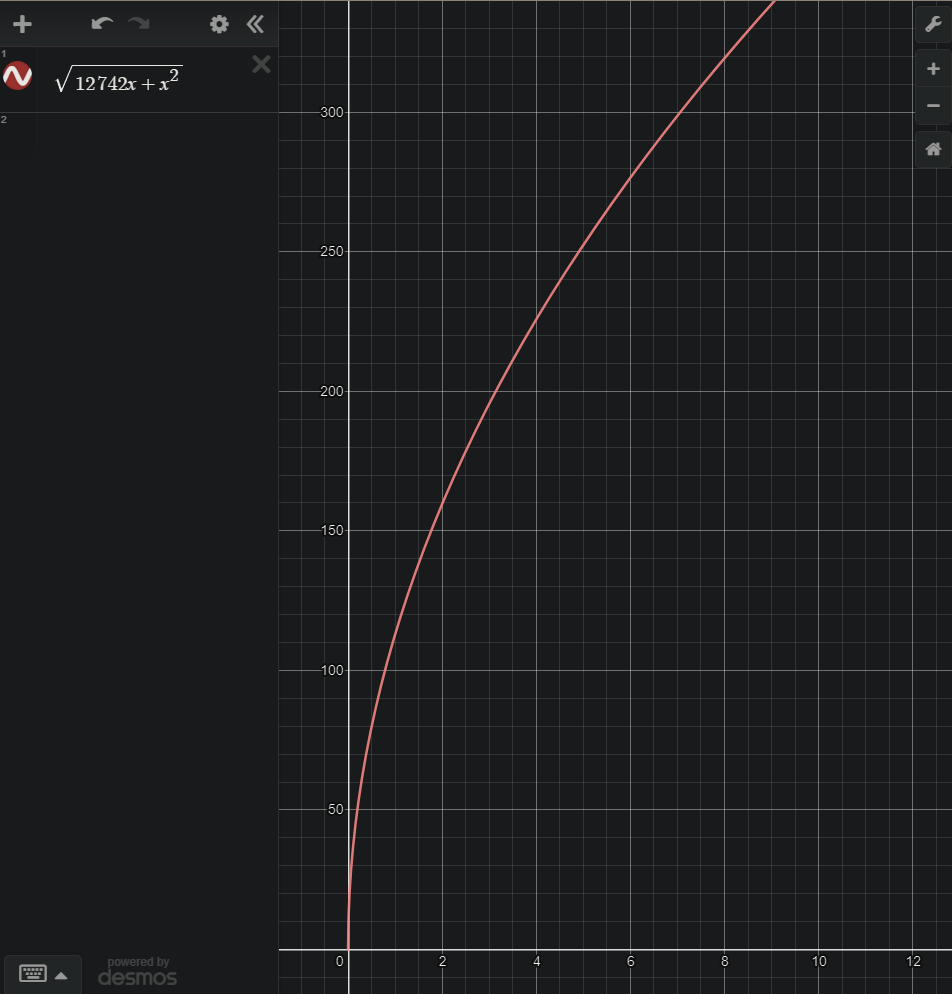
Example for h=1 Km: $$d=\sqrt{1^2+12742}=112.885 Km$$


2. Perimeter of a circle
- Perimeter of a circle $$C=2 \pi R$$
- Angle per unit (radians per kilometer): $$\alpha_{Km}=\frac{\alpha_T}{C}=\frac{2 \pi}{2 \pi R} = \frac{1}{R}$$
- Angle for given distance (d): $$\alpha=\alpha_{Km} \cdot d$$
- Calculation of height h:
$$h = r \cdot (1 - cos(\alpha)) = r \cdot \left(1-cos\left(\frac{d}{R}\right)\right)$$
- Example for d=113 Km $$ h = 6371 \cdot \left(1 - cos \left(\frac{113}{6371} \right)\right) = 1.002 Km$$
3. Trigonometry
- Formules $$sen^2(α)+cos^2(α)=1$$ $$cos(α)=\frac{R}{R+h} \approx \frac{R-h}{R}$$ $$sen(α)=\frac{d}{R+h}$$ $$tg(α)=\frac{d}{R}$$
- By clearing the tangent and the cosine $$tg(α)=\frac{d}{R} \Rightarrow \alpha=arctg(\frac{d}{R})$$ $$cos(α)=\frac{R}{R+h} \Rightarrow h=R \cdot (sec(α)-1)$$ Sustituyendo para d=113 Km, hallar α y h: $$\alpha=arctg(\frac{113}{6371})$$ $$h=6371 \cdot\left(\frac{1}{arctg(\frac{113}{6371})}-1\right)=1.187 Km$$
- Using the second cosine formula $$cos(\alpha)=\frac{R-h}{R} \Rightarrow h=R \cdot (1-cos(\alpha))$$ Sustituyendo para d=113 Km: $$h=6371 \cdot \left(1 - cos\left(arctg \left(\frac{113}{6371}\right)\right)\right)=1.001 Km$$
Python program
1. Pythagorean Theorem
# Pythagorean theorem with observer height, input (d, h0, R) & output (h1)
from numpy import*
# Data: R, h0, h1, d, d1 with same unit (e.g. Km)
## hR: elevated area along all the distance. Example: if the observer and object are separated at the shore of a lake at 200 m of altitude,
## the height is the same along all the distance and is not at sea level, so would be hR = 0.2 Km. (Default hR = 0, sea level)
# User data in same unit (Km)
d = 30
h0 = 0.01 # h0 = 0.01 Km = 10 m
hR = 0
R = 6371 + hR
# Pythagorean theorem:
# d2 = d - d1, (R+h0)^2=d1^2+R^2 and (R+h1)^2=d2^2+R^2
d1 = sqrt(h0**2+(2*R*h0))
h1 = sqrt((d-d1)**2+R**2)-R
print("The distance to the geometrical horizon is %.3f Km and the hidden height is %.3f Km" % (d1, h1))
2. Trigonometry
# Trigonometry at sea level
from numpy import*
# Data: R, h1 (same units, e.g. Km)
R = 6371
h1 = array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]) # Target hidden height
# Target distance : d
d = R*arccos(R/(R+h1))
# Print the result
for i in range(len(h1)):
print("The hidden height is %.1f Km for a distance of %.2f Km" % ((h1[i], d[i])))
3. Perimeter of a circle
# Angle of curvature of a given perimeter, at sea level.
from numpy import*
## Input data (same units, e.g. Km)
R = 6371
C = 2*pi*R # C=12742*pi=40030.14 Km
d = 30
# Angle (in degrees) per unit, convert python defaults radians to degrees
alfa_km = 2*pi/C
# Angle for given distance (d):
alfa = alfa_km*d
# Calculus of the hidden height h1:
h1 = R*(1-cos(alfa))
print("At a distance of %.2f km at sea level the hidden height by curvature is %.2f km." % (d, h1))
Conclusion
The above methods of calculation vary but all give a very similar result. For very high heights the calculations by Pythagoras are not so correct and the second (negative) result of the square root appears. In addition it must be taken into account that in the spherical model nothing could be seen beyond the distance of the radius, since the visible face of the sphere is at most an angle of 90º from the vertical.